Bayes' Theorem

← Conditional Probability

As a data scientist, it will be common for us to need to know the probably of a event (our hypothesis or h) given some existing data (D). It will be very common that we will NOT know the probability. Mathematically, we would express this probability we want to find as P(h|D).

Bayes' Theorem -- commonly also referred to as Bayes' Rule or Bayes' Law -- is a mathematical property that allows us to express a conditional probability in terms of of the inverse of the conditional:

Bayes' Theorem

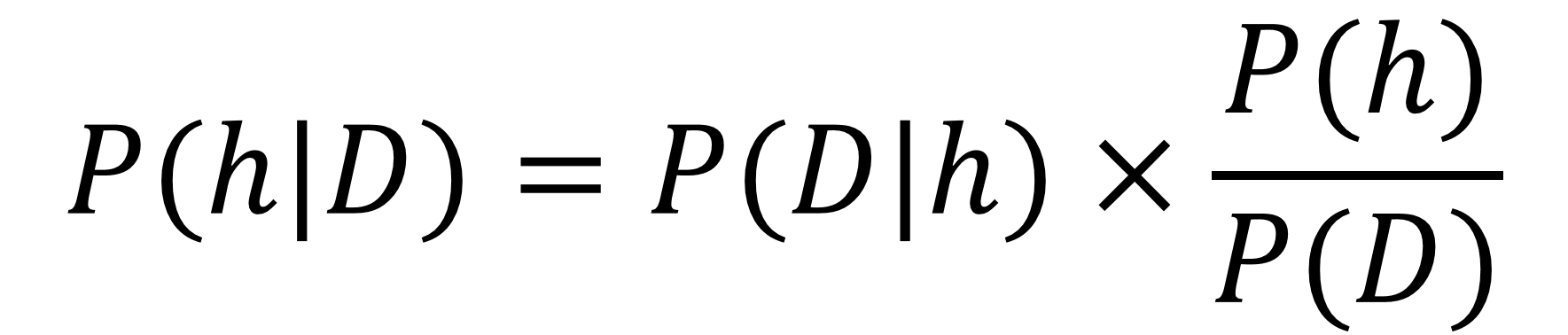
Derivation:

The probability of two events A and B happening is the probability of A times the probability of B given A:
P(A ∩ B) = P(A) × P(B|A)
The probability of A and B can also be written as the probability of B times the probability of A given B:
P(A ∩ B) = P(B) × P(A|B)
We can set both sides of these equations equal to each other:
P(B) × P(A|B) = P(A) × P(B|A)
And solving for the probability of A given B we get:
P(A|B) = P(A) × (P(B|A)/P(B))
This equation is known as the Bayes' Theorem.

Example: Clouds at Sunrise and Rain

We want to predict the probability it will rain in a given day based only on if there are clouds at sunrise. In this example, our hypothesis is that it will rain and our data is that there are clouds at sunrise. Therefore, we're answering the question: P( rain | clouds at sunrise ).

Unfortunately, we only know:

  • It rains 25% of all days, or P(rain) = 25%,
  • It is cloudy at sunrise only 15% of days, or P(clouds at sunrise) = 15%,
  • From our data, we discovered there were clouds at sunrise on 50% of the days it rained, or P(clouds at sunrise | rain) = 50%

This is a classic application of Bayes` Theorem since we have a dataset about the information described by our conditional probability! Applying this problem to Bayes' Rule:

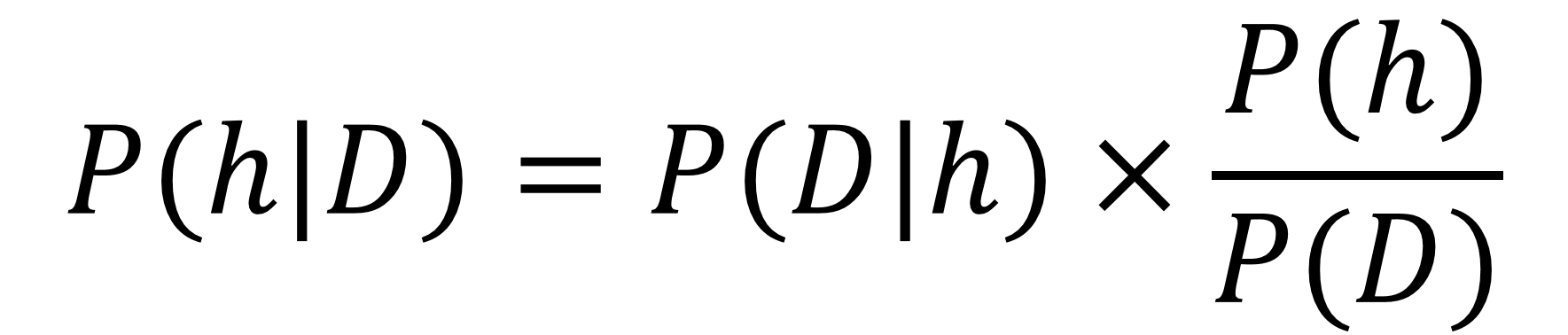
Bayes' Theorem, as applied to Example 1 with Emojis

Solving the formula with the data we know:

  • P(rain | clouds at sunrise) = ???
    ...using Bayes' Theorem...

  • = P(clouds at sunrise | rain) × ( P(rain) / P(clouds at sunrise) )
    ...we know that there is a 50% of chance of clouds at sunrise on days where it rained...

  • = 50% × (P(rain) / P( clouds at sunrise) )
    ...we know the probability of rain on any day, with no conditionals, is 25%...

  • = 50% × ( 25% / P( clouds at sunrise) )
    ...we know the probability of clouds at sunrise on any day, with no conditionals, is 15%...

  • = 50% × ( 25% / 15% )
    ...solving the equation:

  • = 83.33%
    ...and finally, stating the complete answer:

  • P(rain | clouds at sunrise) = 83.33%

This is a really useful result -- if we had no information at all, we only know there's a 25% chance of rain. However, by spotting clouds at sunrise, we know there's now over an 80% probability it will rain!

Example Walk-Throughs with Worksheets

Video 1: Bayes' Rule Examples

Follow along with the workseet to work through the problem:

Practice Questions

Q1: What is an equivalent way to write the following probability using Bayes Theorem?: P(Slept past 10:00 AM | Saturday)
Q2: How would you fix the following Bayes Theorem equation?: P(Went to Jarling's | Eating ice cream) = P(Eating ice cream | Went to Jarling's) / (P(Went to Jarling's) x (P(Eating ice cream))
Q3: What would be the hypothesis and data of the following probability question?: P(Went to Jarling's | Eating ice cream)
Q4: Which of the following probabilities would not be useful to know when trying to calculate the probability that you like a movie given that it is a comedy?
Q5: You want to be able to predict the probability that it is Saturday based on if you slept past 10:00 AM. What would be the correct way to write this probaility in mathematical notation?
← Conditional Probability