Multi-event Probability: Multiplication Rule
Sometimes, we may want to look at more complicated probabilities, such as the probability that two things happen at the same time. To do this, we can use The Multiplication Rule.
When we have two independent events, the Multiplication Rule is:
When A and B are independent events
Example: Rolling Two Dice
The probability of rolling two dice and getting one marked "1" and one marked "2"" can be found using the Multiplication Rule:
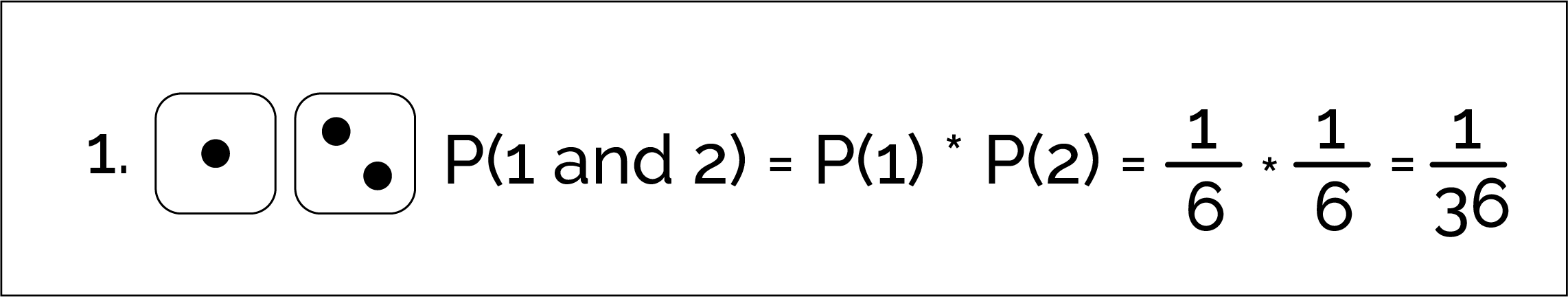
Multiplication Rule (Dependent Events)
For dependent events, the multiplication rule is
P(A and B) = P(A) * P(B | A), where P(B | A) is the probability of event B given that event A happened.
When P(B | A) is the probability of event B given that event A happened.
Example: Drawing Two Cards without Replacement
The probability of drawing 2 cards without replacement from a deck and getting a heart and then a spade can be found using the Multiplication Rule.

Example: Flipping Four Coins
The multiplication rule can be used for more than 2 events as well. Here's a simple example with flipping a fair coin.
For example, what’s the probability of flipping a fair coin 4 times and getting all heads?
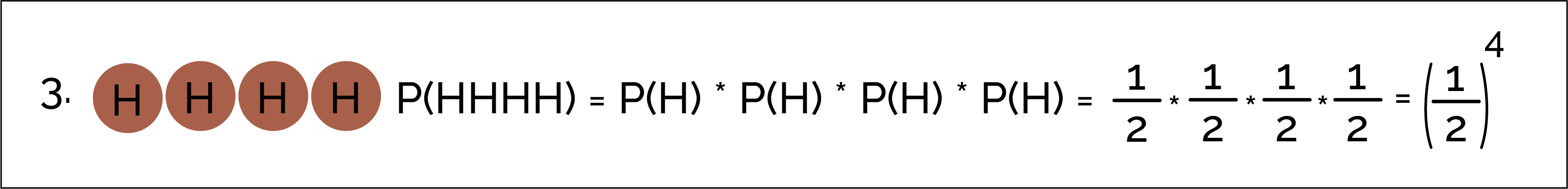
Practice Questions
Q1: When you read a word problem about probability, the word 'and' signals that you should use the multiplication rule.Q2: Which of the following is correct when describing a full, normal deck of cards?
Q3: What is the probability of drawing two cards **with replacement** from a deck and getting a spade and a club
Q4: What is the probability of drawing two cards **without replacement** from a deck and getting a heart and a diamond?
Q5: What is the probability of rolling three dice and getting the first one marked as 1, the second one marked as 2, and the third one marked as three?