Sample Space
Sometimes it is helpful to list all of the possible ways that a chance process can turn out.
Sample Space
In statistics, the sample space is the set of all possible outcomes of an event. For example, the sample space of rolling a fair six-sided die is shown below:

We can also look at the sample space for rolling two fair six-sided dice. The image below shows the 36 possible outcomes for rolling two fair six-sided dice.
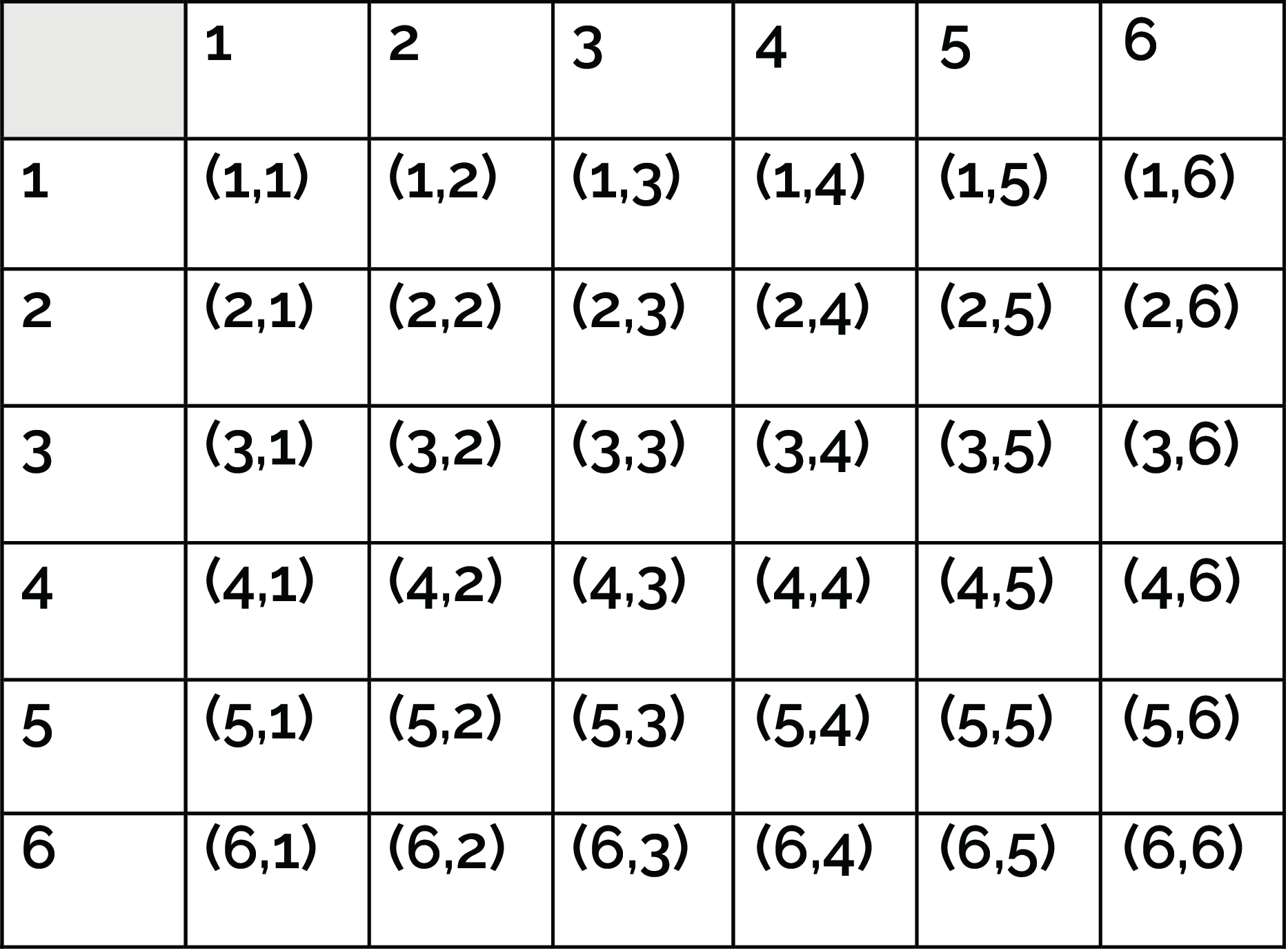
Understanding the idea of sample space can help us calculate probabilities. We know that the probability of a certain outcome can be written as: P(outcome) = # of that outcome / total # of possibilities
The sample space can help us find the numerator and denominator of probabilities.
Example Walk-Throughs with Worksheets
Video 1: Sample Space and State Space
Follow along with the worksheet to work through the problem:
Practice Questions
Q1: Say we are rolling 2 dice. What is the probability that at least one die lands on a 2?Q2: What is the sample space of flipping 5 coins?