Conditionals in Python
Similar to for-loops in Python, conditionals provide a mechanism to control the flow of execution of a program in many programming languages. In Python, the if-statement will run a section of code if and only if the conditional provided is true.
Many people consider 7 to be a lucky number. The Python code below uses an if statement to print out a message if Python randomly choose a lucky number:
Number: 3
There are a few features to notice:
- The line of code begins with an
if, then followed by a conditional, and ends with a colon (:). - The block of code following the
ifstatement is indented. This indentation defines the block of code that will run ONLY if the conditional is true. - The code after the if-statement, back at the original indentation, will only run after the for-loop finishes running.
Notice the two different outputs of the same code based on the randomly generated value:
num = random.randint(1, 10)
if num == 7:
print("Today")
print("is")
print("Your Lucky Day!")
print(f"Number: {num}")Number: 3
The output when the randomly generated number is NOT a 7.
Today is Your Lucky Day! Number: 7
The output when the randomly generated number is a 7.
Conditional Syntax
In Python, the conditional component of an if-statement is nearly identical to the conditionals you have used with Pandas except that you are no longer working within the context of a DataFrame.
- You will use
ifstatements to compare the values of individual variables in Python (ex: values as part of a simulation) instead of values in a DataFrame. - You can still use the six logical operators,
==,>,>=,<<=, and!. - You can still combined multiple conditionals, except you must use
andandor(instead of&and|).
else Statement
Often you may want to run different code when a conditional is true and false. To run code when the conditional is false, an else statement is used. Since else is a control flow statement, it needs a colon (:) at the end and nothing else!
flip = random.choice(["heads", "tails"])
if flip == "heads":
print("Your coin flipped heads!")
else:
print("Your coin flipped tails!")Your coin flipped heads!
The output when the value of flip was randomly choose to be heads.
Your coin flipped tails!
The output when the value of flip was randomly choose to be tails.
Application of if-statements: Conditional Data on Simulation
One of the most useful applications of conditionals is to add conditional data to your DataFrame. For example, roulette is a classic casino game that involves a wheel with 38 equal-sized wedges: 18 red wedges, 18 black wedges, and 2 green wedges.
A simulation of your profit playing roulette while betting on red can be done by a conditional that checks if you the result of the game was red:
- If the result was red, you gain $1. (You get your $1 bet back and gain $1 from the casino.)
- If the result was NOT red, you lose $1. (You lose your $1 bet.)
Running this as a simulation:
color profit 0 black -1 1 red 1 2 red 1 3 black -1 4 red 1 ... ... ... 9995 red 1 9996 red 1 9997 black -1 9998 black -1 9999 red 1
Simulation of 10,000 games of roulette, using a conditional to set the correct value for profit.
df["profit"].sum()-342
The result of this simulation is a loss of $342 after 10,000 games. (The casino always wins.)
Example Walk-Throughs with Worksheets
Video 1: Examples of Conditionals in Python
Practice Questions
Q1: In which case would "Here" print in the following if-statement?
Q2: Which of the following is not part of the correct syntax for an if-statement?
Q3: What would the value of n be after running the following code chunk?

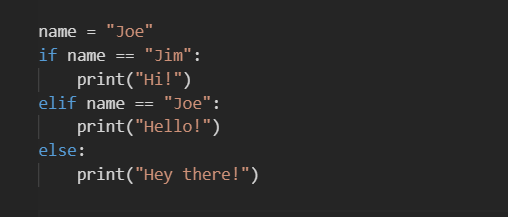
Q5: What would print after running the following code chunk?
